next up prev
Next: 4.iii Further extensions of the Schubert calculus
Up: 4. The Schubert Calculus: Table of Contents
Previous: 4.i. The Schubert Calculus of Lines

4.ii. The Special Schubert Calculus

More generally, we may ask how many linear subspaces of a fixed dimension meet general linear subspaces L1, L2, ..., Ls. We formulate this question in terms of linear subspaces of a vector space.

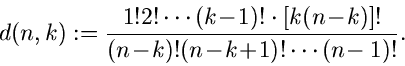
The set of k-dimensional subspaces (k-planes) of an n-dimensional vector space forms the Grassmannian of  k-planes in n-space, Gr(k, n), which is a smooth projective variety of dimension k(n - k). Those k-planes meeting a linear subspace L of dimension n-k+1-l non-trivially (that is, the intersection has positive dimension) form the special Schubert subvariety X(L) of Gr(k, n) which has codimension l. The special Schubert calculus is concerned with the following question.

Question 4.3   Given general linear subspaces L1, L2, ..., Ls of Cn where the dimension of Li is n-k+1-li and we have l1 + l2 + ... + ls equal to k(n - k), how many k-planes K meet each subspace Li non-trivially, that is, satisfy
K meets Li non-trivially, for each i=1, 2, ..., s ? (4.2)

The condition (4.2) is expressed in the global geometry of Gr(k, n) as the number of points in the intersection of the special Schubert varieties

X(L1), X(L2), ..., X(Ls), (4.3)

when the intersection is transverse. (A general theorem of Kleiman [Kl1] guarantees transversality when the Li are in general position, and also implies transversality for the other intersections considered in this section.)

There are algorithms due to Schubert [Sch4] (when each li is 1) and Pieri [Pi] to compute the expected number of solutions. When each li is 1, Schubert [Sch2] showed that the number of solutions is equal to


A line in Pn is a 2-plane in (n+1)-space and two linear subspaces in Pn meet if and only if the corresponding linear subspaces in (n+1)-space have a non-trivial intersection. Thus the problem of lines in projective space corresponds to the case k=2 of the special Schubert calculus. While the geometric problem generalizes easily from k=2 to arbitrary values of k, the proof of Theorem 4.2 does not. There is, however, a relatively simple argument that this special Schubert calculus is fully real.

Theorem 4.4 ([So5 Theorem 1)   Suppose n, k, and l1, l2, ..., ls are positive integers with l1 + l2 + ... + ls equal to k(n - k). Then there are linear subspaces L1, L2, ..., Ls of Rn in general position with the dimension of Ls equal to n-k+1-li such that each of the a priori complex k-planes K satisfying (4.2) are in fact real.

We present an elementary proof of this result in the important special case when each li equals 1 so that the conditions are simple, meaning each Special Schubert variety X(Li) is a hypersurface in the Grassmannian (has codimension 1). This proof generalizes to show that some other classes of enumerative problems in the Schubert calculus are fully real (see Sections 4.iii.b, 4.iii.c, and 4.iii.d ). This generalization constructs sufficiently many real solutions using a limiting argument, as in Section 2.iii.a. Just as the arguments of Section 2.iii.a. were linked to the homotopy algorithms of Huber and Sturmfels, the proof of Theorem 4.4 leads to numerical homotopy methods for solving these problems [HSS,HV].

Subsections
4.ii.a. Geometry of Grassmann Varieties
4.ii.b. Degrees of Schubert Varieties
4.ii.c. Proof of Theorem 4.4
next up prev
Next: 4.iii Further extensions of the Schubert calculus
Up: 4. The Schubert Calculus: Table of Contents
Previous: 4.i. The Schubert Calculus of Lines