Next: 2.iii.b. Fewnomial Upper Bounds
Up: 2.iii. Real Solutions to Sparse Polynomial Systems
2.iii.a. Constructive Lower Bounds
By the example in Section 2.ii.a, if
P is the convex hull of
v0, v1, ..., vn,
a lattice simplex with no interior lattice points, then
a general system (2.1) is equivalent to
the system of binomials
|
y1d1 = a1,
y2d2 = a2,
..., yndn = an
. |
(2.5) |
with each ai non zero.
Here, d1, d3, ..., dn
are the invariant factors of the matrix whose ith column is
vi - v0 and
d1d3...dn
is the normalized volume of P.
Following Sturmfels [Stu1], let
e(P) be the number of these invariant factors which are even.
If e(P)=0, so that d is odd, then P is an odd
cell.
Proposition 2.5
The polynomial system (
2.5) has
2
e(P) real
solutions if
ai > 0 whenever
di is even, and
no real solutions otherwise.
In particular, if
P is an odd cell, then there is at least one real
solution.
Theorem 2.6 (Sturmfels [
Stu1, Corollary 2.3])
The maximum number
r(
P) of real solutions to a sparse
polynomial system (
2.1) with common
Newton polytope
P is at least the the number of odd cells in
any regular triangulation
Pw of
P.
Proof.
In the limit as t approaches zero, the lifted system (2.4) given by a
regular triangulation Pw of P becomes the
disjunction of facial subsystems
of (2.1), one for each facet
F of Pw.
Thus the number
of real solutions in the limit is a constructive lower bound for
r(P).
By Proposition 2.5, the number of odd cells
in Pw is a
lower bound on the number of real solutions to the facial subsystem given by
the facets of Pw.
Q.E.D.
Proposition 2.5 also gives an upper
bound on the
limiting number of real solutions r of the lifted
system (2.4) as t approaches
zero (this is due to Sturmfels [Stu1,
Theorem 2.2].)
|
r is at most | 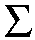 |
2e(F) , |
|
(2.6) |
the sum over all facets F of the regular triangulation
Pw of P.
More sophisticated accounting of the possible signs of the coefficients of
facial subsystems improves this bound.
This accounting is accomplished in [PS] and [IR], leading to a
combinatorial upper bound for such limiting systems.
Itenberg and Roy [IR] show there
is a system (2.1) for
which this upper bound is attained, and thus this combinatorial upper bound
for limiting systems is a lower bound for r(P), the maximum
number of real solutions to a system with common Newton polytope P.
Itenberg and Roy then conjectured that this combinatorial bound was in
fact the global bound, that is, they conjectured that the maximal number of
real solutions occurs in limiting systems.
They also gave a similar bound for r+(P), the number
of solutions with positive coordinates.
This was too optimistic, for Li and Wang [LW] found a
remarkably simple counterexample to this conjecture of Itenberg and Roy
y - x - 1 =
200 - 100y3 + 900x3 -
x3y3 = 0 .
This system has 3 positive solutions
(0.317659, 1.317659), (.659995, 1.659995),
and (8.12058, 9.12058) ,
but the combinatorial upper bound is 2.
Thus systems with the maximal number of real solutions cannot in general be
constructed with these limiting techniques.
We still have more questions than answers.
Among the questions are:
- Improve this lower bound for r(P) (or for
r+(P) of Itenberg and Roy.
- Find new general methods to construct systems with many real solutions.
- Determine which polytopes P have the property that
r(P) < n!VolP, that is, not all the
solutions can be real.

Next: 2.iii.b. Fewnomial Upper Bounds
Up: 2.iii. Real Solutions to Sparse Polynomial Systems