2.v. Equivalent systems

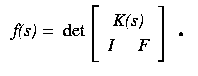
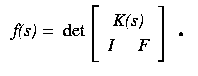   First, our choice of F as local coordinates for the Grassmannian is not canonical, and any other choice will give an equivalent system of polynomials. We caution that for some choices of the parameters s₁, s₂, ..., s_mp, there may be solutions that do not lie in the chosen coordinate patch.

   More interesting is the matrix K(s). The first row consists of all monomials of degree less than m+p, and subsequent rows are derivatives of the first. The first row is a parameterization of a rational normal curve in C^m+p, and so it follows that K(s) is the m-plane osculating this curve. Since all parameterized rational normal curves are projectively equivalent, we are free to replace K(s) in the definition of f(s) above by any m-plane osculating a parameterized real rational normal curve. (This is equivalent to choosing different local coordinates for the Grassmannian.)

   Reparameterizing the original rational normal curve, we may assume that up to 3 of the s_i are any fixed points on the projective line. It is most useful to fix one to be 0 and one to be the point at infinity. Doing so, we may reduce the parameters by 2, and choose local coordinates for the set of p-planes H which meet the m-plane osculating at 0 and infinity. For details on the selection, see Section 2.5 of "Real Schubert Calculus: Polynomial systems and a conjecture of Shapiro and Shapiro". We have a Maple script that will generate local coordinates.