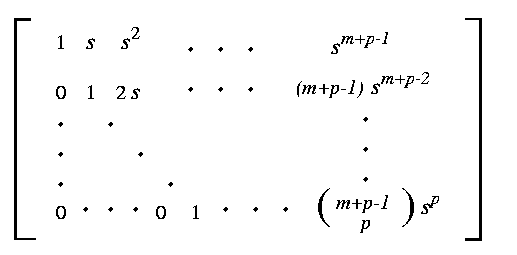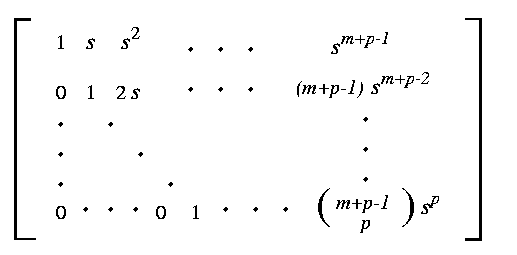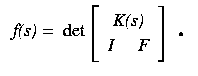2.ii. The conjecture of Shapiro and Shapiro
Boris Shapiro and Michael Shapiro made a precise conjecture which asserts
that if the m-planes K1, ..., Kmp are
chosen in a particular fashion, then all dm,p
p-planes H which meet each Ki nontrivially
are real.
Let K(s) be the following m by (m+p)-matrix of
polynomials:
(Also the row space of the same matrix, a m-plane.)
Let f(s) be the polynomial
Conjecture 1. (Shapiro-Shapiro)
If s1, s2, ..., smp are general
distinct real numbers, then each of the dm,p solutions to
the system of polynomials
|
f(s1) = f(s2) = ... = f(smp) = 0
|
is real.
Equivalently, every p-plane H
which meets each K(si) nontrivially is real.
This is true when (m,p)=(2,2).
We have a Maple V.5
script,
which, when run, proves this assertion.
Here is its output.