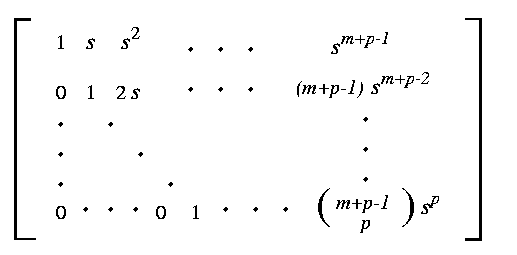2.iv. Shapiro's Conjecture and the placement problem
An important variant of the pole placement problem is that
when the matrices A, B, and C are real, and
when f(s) has all (mp) roots real, which (if any) real
feedback laws satisfy
|
f(s) = det(sIn - A - BFC).
|
Using the coprime factorization N(s)D(s)-1
of the transfer function, as in Section 2.iii,
and letting s1,s2,...,sn
be the (real) roots of the polynomial f,
the real pole placement problem is equivalent to the following
question:
Which real m by p-matrices F satisfy
for each i=1, 2, ..., n?
The conjecture of Shapiro and Shapiro is then seen to be a special case of
the real pole placement problem.
Let n=mp and note that the matrix K(s) of their conjecture:
has the same form as the top submatrix in the previous equation.