Next: 6.ii. Lower bounds in the Schubert Calculus for flags?
Up: 6. Lower bounds in the Schubert calculus

6.i. Real Degree of Grassmann Varieties

Recall from Section 4.ii that the k-planes in Cⁿ meeting k(n-k) general (n-k)-planes non-trivially is a complementary dimensional linear section of the Grassmannian, the intersection of Gr(k,n) with a linear subspace M of codimension k(n-k). The number of such k-planes is the degree d(k,n) of the Grassmannian Gr(k,n). This is also the degree of the linear projection

q_E : Gr(k,n) ----> P^k(n-k)

with center of projection a plane E in Plücker space having codimension k(n-k)+1 that is disjoint from Gr(k,n). The connection between these two definitions of degree is that when E is a subset of M, q_E(M) is a point x in P^k(n-k) and the intersection of M with Gr(k,n) is q_E^-1(x). Since complex manifolds are canonically oriented, the degree of such a linear projection is just the number of points in the inverse image of a regular value x.

An important such linear projection is the Wronski map. Let L(t) be the (n-k)-plane osculating the rational normal curve (5.1). By (4.6) and the discussion following Theorem 5.2, the equation for a k-plane K to meet L(t) non-trivially is

t^{n(n+1)/2 - k(k+1)/2 - |a|} L_a p_a(K) ,

(6.1)

where p_a(K) is the ath Plücker coordinate of K and L_a is the appropriately signed Plücker coordinate of L(0) complementary to a. The association of a k-plane K to the polynomial (6.1) is the Wronski map

q_W : Gr(k,n) ----> P^k(n-k) ,

where P^k(n-k) is the space of polynomials of degree at most k(n-k), modulo scalars. This is a linear projection as the coefficients in (6.1) are linear in the Plücker coordinates. If a polynomial f(t) of degree k(n-k) has distinct roots t₁, t₂, ..., t_k(n-k), then q_W^-1(f) is the set of k-planes meeting each of L(t₁), L(t₂), ... L(t_k(n-k)) non-trivially.

To see why this is called the Wronski map, consider Gr(k,n) as the set of k-planes in the space of polynomials of degree at most n-1. Given a k-plane

K = linear span { f₁, f₂, ..., f_k } ,

the Wronski determinant of K is

W(K) = det

f₁	f₂	...	f_k
f'₁	f'₂	...	f'_k
.	.		.
.	.		.
f₁^(k-1)	f₂^(k-1)	...	f_k^(k-1)

which is a polynomial of degree at most k(n-K), well-defined modulo scalars. Under a choice of coordinates given by the coefficients of a polynomial, W(K) = q_W(K).

Since real manifolds are not necessarily orientable, the degree of a map is a Z/2Z-valued invariant. However, Kronecker [Kr] defined the degree of a regular map RP² --> RP² which he called the characteristic, and his definition makes sense for many maps f : X --> Y of (not necessarily orientable) compact manifolds.

First suppose that X is oriented. For a regular value y in Y of f, define

char(f) :=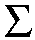

sgn( det df_x ) ,

the sum over all x in f^-1(y), using local coordinates in X consistent with its orientation and any local coordinate near y in Y. The sum is well-defined up to multiplication by -1, and so may take its absolute value as our invariant. This number is independent of choices, if Y is connected.

When X may not be orientable, let oX --> X and oY --> Y be the canonical spaces of orientations of X and Y, which are 2 to 1 coverings with covering group Z/2Z. These spaces of orientations are canonically oriented. The map f is orientable if it has a lift of : oX --> oY that is equivariant with respect to the covering group Z/2Z. Define the characteristic of an orientable map f to be the characteristic of the orienting lift, of. This is well-defined, even if oY consists of 2 components. This characteristic satisfies a fundamental inequality.

Proposition 6.2 Let f : X --> Y be an orientable map. Then, for every regular value y in Y,

# f^-1(y) is at least char (f) .

We call this characteristic the real degree of the map f

Consider this notion for the Wronski map of the real Grassmannian Gr_R(k,n). The Grasmannian has dimension k(n-k) and is orientable if and only if n is even. Eremenko and Gabrielov [EG2] compute the degree of the Wronski map. To state their main result, we introduce some additional combinatorics. Recall the interpretation (4.9)

degree Gr(k,n) = # { chains in the Bruhat order from 0 to 1 } ,

where 0 = (1, 2, ..., k) is the minimal element in the Bruhat order and 1 = (n-k+1, ..., n-1, n) is the top element in the Bruhat order. We introduce a statistic on these chains. Each cover a < b in the Bruhat order has a unique index i with

a_i < b_i = a_i+1 but a_j = b_j for j not equal to i .

The word w(c) of a chain in the Bruhat order is the sequence of indices (i₁, i₂, ..., i_k(n-k)) of these indices for covers in the chain c. An inversion in such a word is a pair j<l with i_j<i_l, and the weight, |c| is the number of inversions in the word of the chain c. For instance the chain in the Bruhat order of Gr(3,6) highlighted in Figure 11

123 < 124 < 125 < 135 < 145 < 245 < 246 < 346 < 356 < 456 ,

has word 332213121 and length 5. Define the inversion polynomial

I(k,n)(t) :=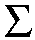

t^|c| ,

the sum over all chains c in the Bruhat order from 0 to 1.

Theorem 6.5 (Eremenko and Gabrielov [EG2, Theorem 1]) The characteristic of the Wronski map q_W : Gr_R(k,n) --> RP^k(n-k) is |I(k,n)(-1)|.

They prove this by an induction reminiscent of that used in the proof of Theorem 4.6. In the course of their proof, they construct a polynomial f with all roots real having d(k,n) (= degree of the Grassmannian) real points in q_W^-1(f) (one for each chain in the Bruhat order) and show that

det dq_W = (-1)^|c| ,

at the point in q_W^-1(f) corresponding to the chain c.

White [Wh] studied the statistic |I(k,n)(-1)| and showed that it equals zero if and only if n is even. The main result of Eremenko and Gabrielov is the following, which gives a lower bound for the number of real solutions in some cases of the Shapiro conjecture.

Corollary 6.6 (Eremenko and Gabrielov [EG2, Corollary 2]) Let L₁, L₂, ..., L_k(n-k) be general codimension (n-k)-planes in Rⁿ osculating the rational normal curve at k(n-k) general real points. Then the number r of real k-planes K meeting each L_i non-trivially lies between |I(k,n)(-1)| and I(k,n)(1)|. In particular, when n is odd this number r is non-zero.

This lower bound holds not only if the osculating planes are real, but if the set of points {t₁, t₂, ..., t_k(n-k)} where they osculate are real (the roots of a real polynomial), which is equivalent to the consition that this set is stable under complex conjugation.

Consider now a linear projection different than the Wronski map. If we move the center E, then the degree of the projection q_E does not change as long as E does not meet the Grassmannian. Thus if E is in the same component of the space of codimension k(n-k)+1 linear subspaces not meeting the Grassmannian as is the center W of the Wronski map, then COrollary 6.6 applies to q_E^-1(x), for x a real point in the image of q_E.

These new ideas of Eremenko and Gabrielov, particularly their notion of real degree, greatly increase our understanding of the real Schubert calculus. We emphasize that this is an important start in the search for lower bounds to other enumerative problems. Not all enumerative problems involve a linear projection of a submanifold of projective space. In fact, of the other enumerative problems we have considered in the Schubert calculus, only those simple Schubert calculus problems on Lagrangian Grassmannians involve linear projections, and they have a lower bound of 0. There has been very little experimental work investigating lower bounds. We describe some of it in the final section.

Next: 6.ii. Lower bounds in the Schubert Calculus for flags?
Up: 6. Lower bounds in the Schubert calculus