

| Phase limit set of the plane in 3-space |  |
 |
|
The coamoeba of the plane is those triples
(θx, θy, θz)
for which there exist a quadrilateral with one side horizontal whose other
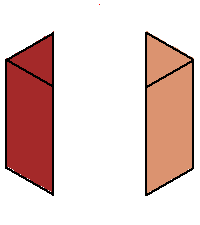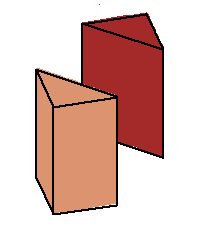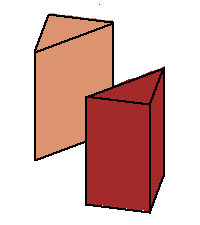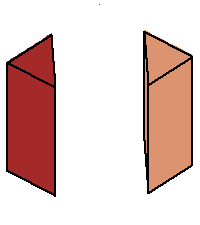
sides make these angles to the horizontal. The phase limit set is the limiting values of these angles as one of the coordinates (x,y,z, or 1) tends to zero. (1→0 when the other three coordinates increase without bound.) From our geometric description of the coamoeba as angles of quadrilaterals, we see that these will be essentially cylinders over the phase limit sets of lines in 2-space, which is what we see below: |
|||
 Phase limit set as x→0 |
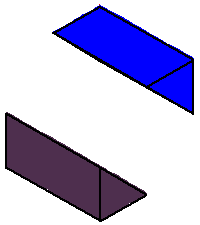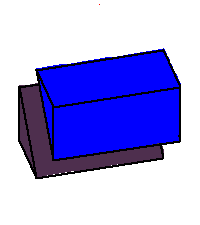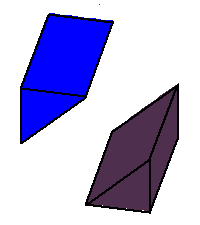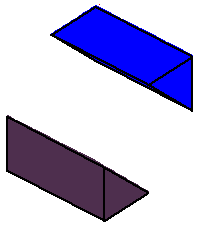 Phase limit set as y→0 |
 Phase limit set as z→0 |
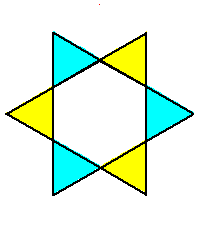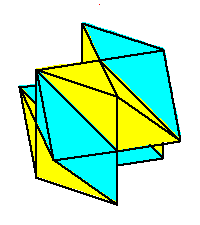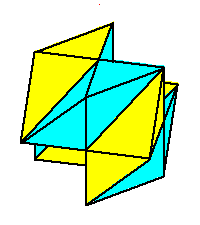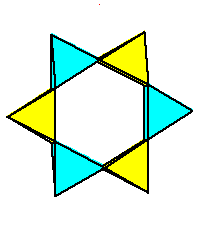 Phase limit set as 1→0 |