Shapiro Conjecture 4: Some Linear Algebra

Some Linear Algebra

This Wronskian is equal to the determinant of square d+1 by d+1 matrix.

If f₁(t), f₂(t), ..., f_k(t) are generic, then row operations convert them to

f₁(t) = t^d -a₁₁t^d-k 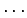-a_1,d-kt -a_1,d+1-k

f₂(t) = t^d-1 -a₂₁t^d-k 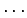-a_2,d-kt -a_2,d+1-k

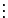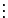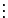f_k(t) = t^d+1-k -a_k1t^d-k 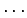-a_k,d-kt -a_k,d+1-k

Set g(t) := (1, t, t², ..., t^d ) and let G(t) be the k by d+1 matrix with rows g(t), g'(t), ..., g^(k-1)(t).
Then the Wronskian of the polynomials f₁(t), f₂(t), ..., f_k(t) is the determinant of

G(t)

A^t I

where I is the identity matrix of size d+1-k, and
A = (a_i,j ) is the k by d+1-k matrix of the coefficients of the polynomials f_i (t).

The lower portion of the matrix (A^t : I ) are linear forms defining the linear span of the polynomials f₁(t), f₂(t), ..., f_k(t).

f₁(t)	=	t^d			-a₁₁t^d-k	-a_1,d-kt	-a_1,d+1-k
f₂(t)	=		t^d-1		-a₂₁t^d-k	-a_2,d-kt	-a_2,d+1-k

f_k(t)	=			t^d+1-k	-a_k1t^d-k	-a_k,d-kt	-a_k,d+1-k