Geometric Interpretation 5
More generally, the Wronskian W(f1(t), f2(t), ..., fk(t)) is the determinant of the matrix
G(t)
H
where the rows of the d+1-k by d+1 matrix H cut out the polynomials f1(t), f2(t), ..., fk(t),
and G(t) has rows g(t), g'(t), ..., g(k-1)(t) where g(t) is the rational normal curve (1, t, t 2, ..., t d ).

    Let F(t) be a polynomial of degree k(d+1-k) with distinct roots s1, s2, ..., sk(d+1-k).
Then the linear spaces of polynomials f1(t), f2(t), ..., fk(t) with Wronskian F(t) are cut out by the solutions H to the system of equations

det
G(si )
H
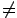 =  0 for each i = 1,...,k(d+1-k).
Writing G(t) and H for the row spaces of the corresponding matrices,
these equations are equivalent to the geometric conditions
G(si )     H   {0}           for each i = 1,...,k(d+1-k).