Bivariate Semialgebraic Splines

Michael DiPasquale and Frank Sottile.

Bivariate Semialgebraic Splines
Macaulay 2 Code for the examples in this paper Its output.

Semialgebraic splines are bivariate splines over meshes whose edges are arcs of algebraic curves. They were first considered by Wang, Chui, and Stiller. We compute the dimension of the space of semialgebraic splines in two extreme cases. If the polynomials defining the edges span a three-dimensional space of polynomials, then we show that the dimensions can be reduced to that of rectilinear meshes. If the mesh is sufficiently generic, we give a formula for the dimension of the spline space valid in large degree and bound how large the degree must be for the formula to hold. We also study the dimension of the spline space in examples which do not satisfy either extreme. The results are derived using commutative and homological algebra.

We display a C⁰-spline and a C¹-spline defined on a rectangle in R² subdivided into eight regions by the two parabolas and the ine segment as shown.


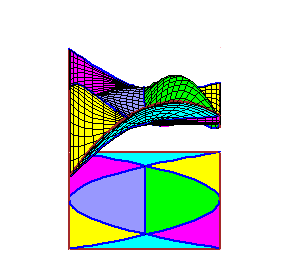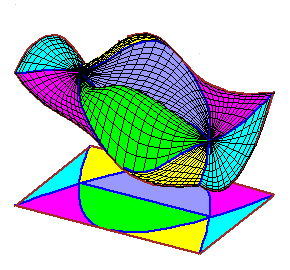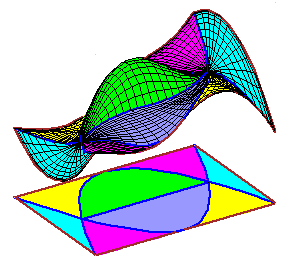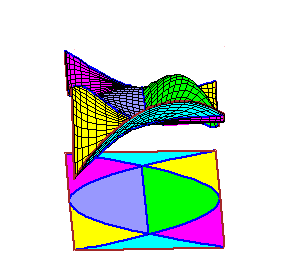
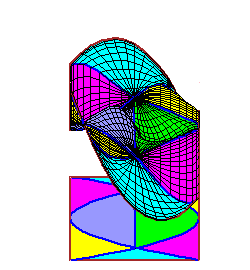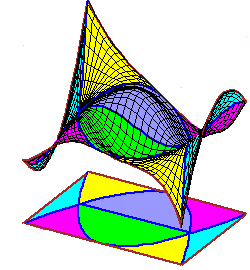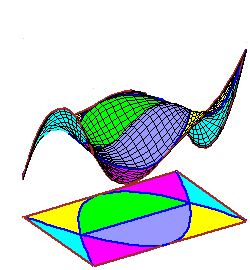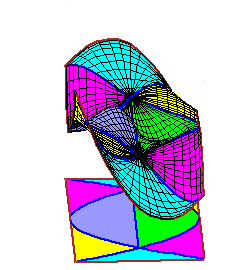
The movies of C⁰ splines were created using the maple file `C0.maple`. The movies of C¹ splines were created using the maple file `C1.maple`.

Last modified: Mon Jan 13 14:45:15 CET 2020