Pencils of Quadrics

Michael DiPasquale, Frank Sottile, and Lanyin (Larry) Sun.

Return to Semialgebraic Splines.

We display cell complexes Δ that subdivide the unit circle with three faces, three edges, and one vertex (at the origin). In these cell complexes the curves underlying the edges form a pencil of quadrics. Such a pencil defines a zero-scheme in CP² of degree four. In our paper we show that when the curves are members of a pencil of curves. the dimensions of the spline modules (their Hilbert functions) do not depend upon the actual edges, but only on their number and degrees. In particular, the geometry of the curves has no effect. The eight cell complexes below illustrate this. Each pencil in the first four defines four reduced points, either four real points in the finite part of CP² or four real points with two at infinity, and then the same with two real and two complex, the second pair being either in the finite part of CP² or at infinity. The others involve one or more double points.

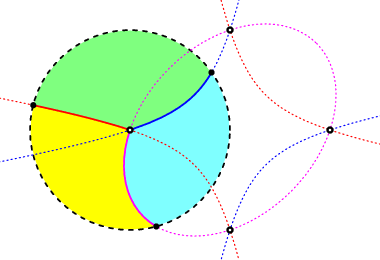
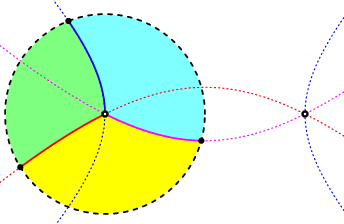
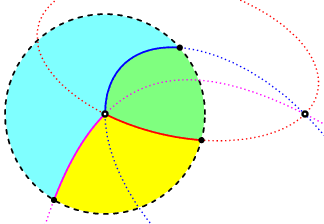
Four real finite points	Four real points, two at infinity	Two real two complex, all finite
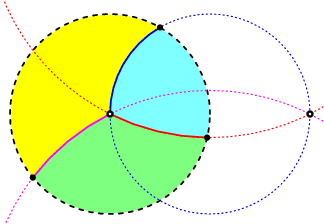
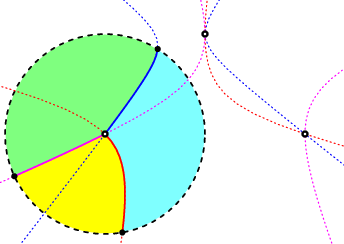
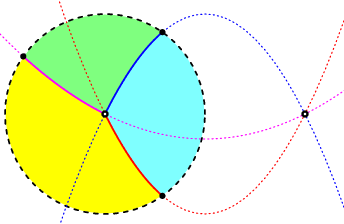
Two complex points at infinity	Two real and one double point	Two real and one double point at infinity
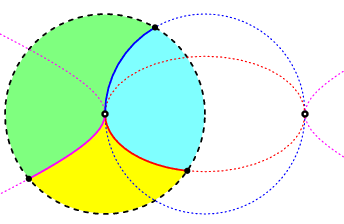
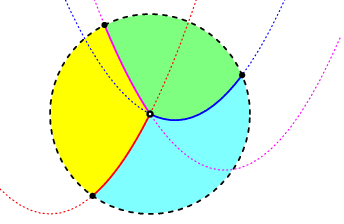
Two real double points	Two real and one triple point at infinity

The following table gives the Hilbert function for all these cell complexes given by three quadrics in a pencil.
They were generated with the Macaulay2 file pencil.m2.

r\d	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36	37	38	39	40
0	1	3	7	13	22	34	49	67	88	112	139	169	202	238	277	319	364	412	463	517	574	634	697	763	832	904	979	1057	1138	1222	1309	1399	1492	1588	1687	1789	1894	2002	2113	2227	2344
1	1	3	6	10	15	21	30	42	57	75	96	120	147	177	210	246	285	327	372	420	471	525	582	642	705	771	840	912	987	1065	1146	1230	1317	1407	1500	1596	1695	1797	1902	2010	2121
2	1	3	6	10	15	21	28	36	46	58	73	91	112	136	163	193	226	262	301	343	388	436	487	541	598	658	721	787	856	928	1003	1081	1162	1246	1333	1423	1516	1612	1711	1813	1918
3	1	3	6	10	15	21	28	36	45	55	66	78	93	111	132	156	183	213	246	282	321	363	408	456	507	561	618	678	741	807	876	948	1023	1101	1182	1266	1353	1443	1536	1632	1731
4	1	3	6	10	15	21	28	36	45	55	66	78	91	105	121	139	160	184	211	241	274	310	349	391	436	484	535	589	646	706	769	835	904	976	1051	1129	1210	1294	1381	1471	1564
5	1	3	6	10	15	21	28	36	45	55	66	78	91	105	120	136	153	171	192	216	243	273	306	342	381	423	468	516	567	621	678	738	801	867	936	1008	1083	1161	1242	1326	1413
6	1	3	6	10	15	21	28	36	45	55	66	78	91	105	120	136	153	171	190	210	232	256	283	313	346	382	421	463	508	556	607	661	718	778	841	907	976	1048	1123	1201	1282
7	1	3	6	10	15	21	28	36	45	55	66	78	91	105	120	136	153	171	190	210	231	253	276	300	327	357	390	426	465	507	552	600	651	705	762	822	885	951	1020	1092	1167
8	1	3	6	10	15	21	28	36	45	55	66	78	91	105	120	136	153	171	190	210	231	253	276	300	325	351	379	409	442	478	517	559	604	652	703	757	814	874	937	1003	1072
9	1	3	6	10	15	21	28	36	45	55	66	78	91	105	120	136	153	171	190	210	231	253	276	300	325	351	378	406	435	465	498	534	573	615	660	708	759	813	870	930	993
10	1	3	6	10	15	21	28	36	45	55	66	78	91	105	120	136	153	171	190	210	231	253	276	300	325	351	378	406	435	465	496	528	562	598	637	679	724	772	823	877	934
11	1	3	6	10	15	21	28	36	45	55	66	78	91	105	120	136	153	171	190	210	231	253	276	300	325	351	378	406	435	465	496	528	561	595	630	666	705	747	792	840	891
12	1	3	6	10	15	21	28	36	45	55	66	78	91	105	120	136	153	171	190	210	231	253	276	300	325	351	378	406	435	465	496	528	561	595	630	666	703	741	781	823	868

Last modified: Thu Feb 18 23:05:59 CST 2016