

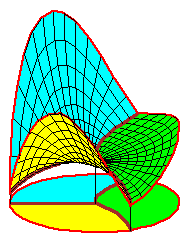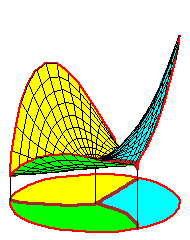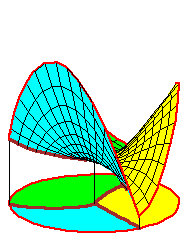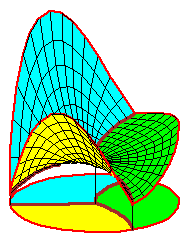



The movies of C1 splines were created using the maple file C1_spline.maple.

|

|

|

|

|

|
|
The movies of C0 splines were created using the maple file
C0_spline.maple. The movies of C1 splines were created using the maple file C1_spline.maple. |
|||||