|
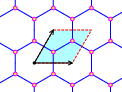
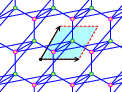
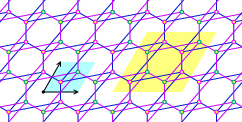
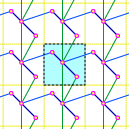
To a Zd-periodic weighted graph with vertices V, we may associate a periodic graph operator that acts on ℓ2(V).
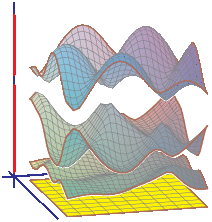
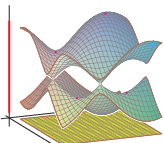
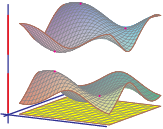
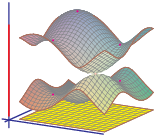
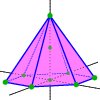
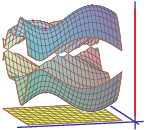
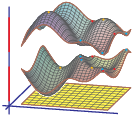
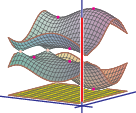
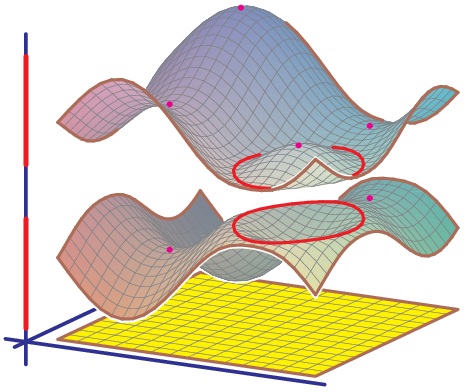
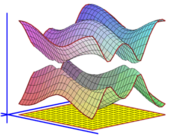
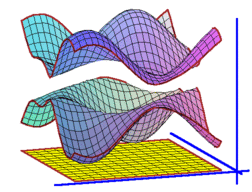
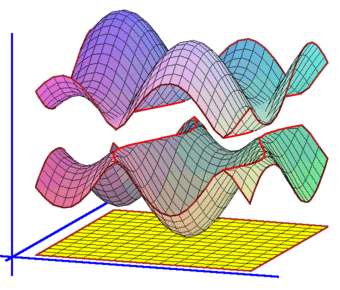
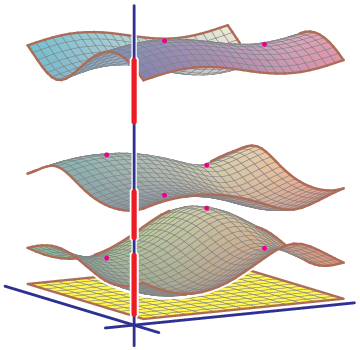
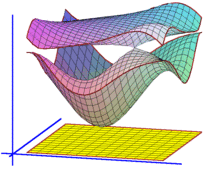
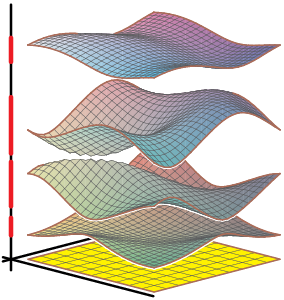
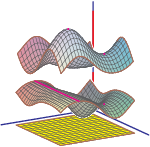
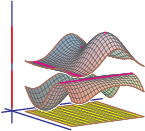
After Floquet transform, we obtain its Bloch variety, which is an algebraic hypersurface in Td×R
whose projection to R is the spectrum of the operator.
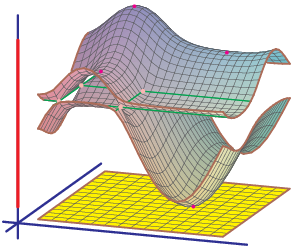
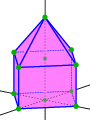
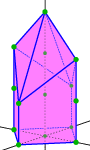
Features on Bloch varieties such as Dirac (double) points, critical points, and their level sets (Fermi varieties)
reflect spectral properties of the operator.
With students Faust and Robinson, and using the Brazos cluster, we investigated
over 2.1 million small periodic graphs, recording invariants and features of their Bloch and Fermi varieties.
In this talk, I will briefly discuss the background and present some examples of interesting behavior of Bloch varieties that we uncovered.
|