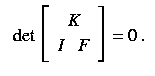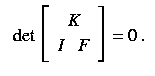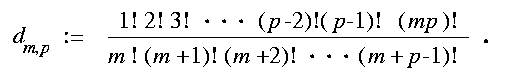2.i. Polynomial formulation of hypersurface Schubert conditions
A hypersurface Schubert condition on p-planes in
Cm+p is the condition that a
p-plane H
meet a fixed m-plane K non-trivially.
We write this in local coordinates for the Grassmannian of p-planes in
Cm+p.
Local coordinates are furnished by a m by p-matrix F of
indeterminates, where H is the row space of the
p by (m+p)-matrix obtained by concatenating an identity matrix
with F.
If we consider K to be the row space of a
m by (m+p)-matrix, then the condition that H meet K
nontrivially is
According to the Theorem of Schubert [Sc],
and Kleiman's Transversality Theorem
[Kl],
if K1,...,Kmp are in general position, then
there are
p-planes H which meet each Ki nontrivially.
In particular, the resulting system of mp determinants in the
mp indeterminates given by F has dm,p
solutions.