Back:
Hyperboloid Through Three Tangent Lines
Up:
The Shapiro Conjecture
The Fourth Tangent Line
Now consider a fourth line tangent to the rational normal curve.
It is sufficient to consider only those lines tangent at a point along the arc
between the red and
magenta points of tangency of the curve and the
hyperboloid.
(Any of the three arcs may be transformed into one another by a real
Möbius transformation.)
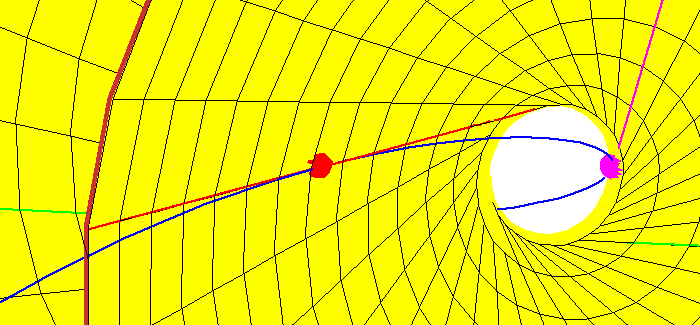
From this closeup, it should be evident that
every such tangent line meets the hyperboloid in two points, which gives two
real lines meeting the four given lines that are tangent to the rational
normal curve.
For skeptics, we have included an animation of this nifty geometric fact.
There are two animations of sizes
1968 KB and
5479 KB.
Last Modified Saturday 20 2003
by Frank Sottile
