where f-1([a, b]) is the cubic curve defined by the polynomial aP + bQ .
Consider the Euler characteristic of Z first over C and then over R. Blowing up a smooth point on a surface replaces it with a P1C and thus increases the Euler characteristic by 1. Since P1C has Euler characteristic 3, we see that Z has Euler characteristic 3 + 9 = 12. The general fibre of f is a smooth plane cubic which is homeomorphic to the 2-torus (S1 x S1), and so has Euler characteristic 0. Thus only the singular fibres of f contribute to the Euler characteristic of Z. Assume that the 8 points are in general position so there are only nodal cubics in the pencil. A nodal cubic has Euler characteristic 1. Thus there are 12 singular fibres of f and hence 12 singular cubics meeting 8 general points in P2C.
Consider now the Euler characteristic of ZR. Blowing up a smooth point on a real surface replaces the point by P1R = S1, and hence decreases the Euler characteristic by 1. Since P2R has Euler characteristic 1, the Euler characteristic of ZR is 1 - 9 = -8. A nonsingular real cubic is homeomorphic to either one or two disjoint copies of S1, and hence has Euler characteristic 0. Again the Euler characteristic of ZR is carried by its singular fibres. There are two nodal real cubics; either the node has two real branches or two complex conjugate branches so that the singular point is isolated. Call these curves real nodal and complex nodal, respectively. They are displayed in Figure 7.
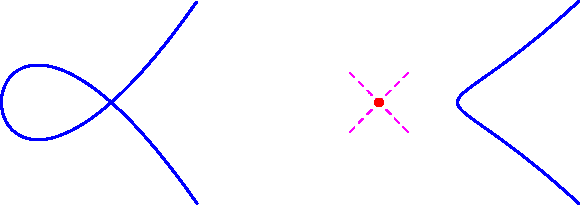 |
| Figure 7: A real nodal and a complex nodal curve |
Among the singular fibres, we have
| -8 | = | #{complex nodal} - #{real nodal}, with | 12 | = | #{complex nodal} + #{real nodal}, |

| ||||
| (y-28)2 | = | 4x3-85x2 +504x-18yx | ||
| (x-28)2 | = | 4y3-85y2 +504y-18xy | ||
| Figure 8: Complex nodal curves meeting in 9 points | ||||
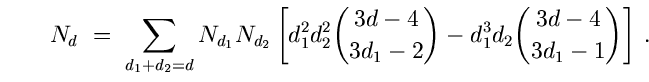
The values N1 = N2 = 1 are trivially fully real, and we have just seen that N3 = 12 is fully real. The next case of N4 = 620 (computed by Zeuthen [Ze1]) seems quite challenging.



Next: 3.v. Lines tangent to Spheres in Rn
Up: 3. Enumerative Real Algebraic Geometry: Table of Contents
Previous: 3.iii. The Stewart-Gough Platform