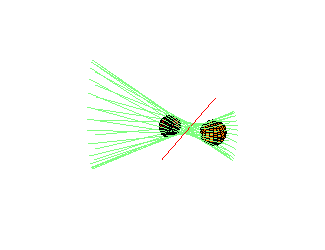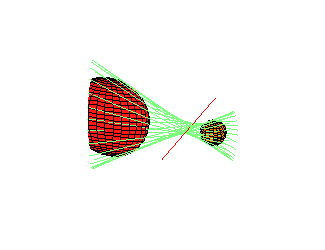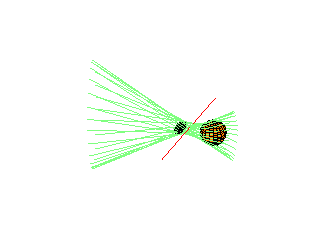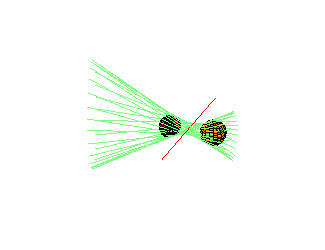
Alternative Geometric Description: This remarkable reducibility (but not the number 12 of components) may alternatively be understood as follows: Fixing l1 and l2, there is an action of the non-zero complex numbers C* on 3-space, preserving common transversals. Each component is one orbit of this action.

Theorem.
All of the geometry discussed here, including number of solutions, number of families, etc., can be achieved over the real numbers.     In particular,
There exist 4 spheres in R³ with 12 common tangents.
There are 2 lines and a hyperboloid with all 12 familes (orbits) real.