Common transversals and tangents to
two lines and a quadric in P3
Gabor Megyesi
Frank Sottile
Thorsten Theobald
24 June 2002

Summary. Given two general lines and two general quadrics in P3, there are exactly 8 lines that simultaneously meet the two given lines and are tangent to the two quadrics. Call these 8 lines common transversals and tangents. Here, we are concerned with the situation when the lines and quadrics are not generic; that is when there are infinitely many such common transversals and tangents. Specifically, which arrangements of lines and quadrics have infinitely many common transversals and tangents.

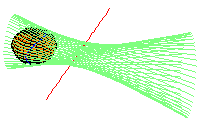
Our approach is to fix two (skew) lines and a quadric, and then describe the common transversals and tangents in this case. For example, the picture above on the left displays the lines transversal to the red line and to a line at infinity, and tangent to the sphere as shown. The curve of tangency is drawn in blue.

Having done that, we then describe which second quadrics have the same set of common transversals and tangents. For example, the picture on the right shows the same sphere, common transversals and tangents, and red line, and it shows a hyperboloid of two sheets tangent to every one of the common transversals and tangent to the sphere. (Here the sphere is hidden in the back of the main figure.)

We study the fascinating geometry behind this in the paper of the same name. Briefly, fixing the two lines and the first quadric, the space of second quadrics for which there are infinitely many common transversals and tangents is a curve in the P9 of quadrics that is remarkable reducible---it is the union of 12 plane conics! This page is dedicated to providing computer algebra scripts used to prove these results and displaying the many (very intriguing) pictures we have generated of this situation.

Table of Contents

  1. Early Version of this Page.
  2. Slides From a Seminar Talk.
  3. Slides From an Invited Talk.
  4. Proof of Main Theorem for Assymmetric (2,2)-curves.
  5. Proof of Main Theorem for symmetric (2,2)-curves.
  6. Pictures of Common Transversals and Tangent to Symmetric Quadrics.
Last modified on 14 July 2002 by Frank Sottile