Home Work 6 Math 344S - Winter 1998

Due: 2 April 1998

1. A Young tableau of size n is an arrangement of the integers 1,2,...,n in a left-justified array, like a Ferres diagram, but with numbers instead of boxes or dots. Also, the numbers increase across each row and down each column. For example, here are some Young Tableaux of size 6:
   
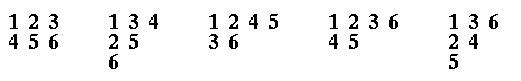
   How many pairs (P,Q) of Young tableaux with P and Q having the same shape are there:
   With size n = 4?
   With size n = 5?
   
2. Which of the following graphs are isomorphic and which are not? The best way to write this up may be the following. First, summarize your findings, eg. "The sets of isomorphic graphs are {A,C,E}, {B,F,J}, {D,I}, {G}, {H}". Then, for the isomorphic graphs, draw them (or display cut out copies) where you have indicated the isomorphisms by labeling. Finally, to show there are no more isomorphisms, do this for one graph in each set, eg. "H cannot be isomorphic to A or B, as H has a pentagon, but A and C do not".
   
   
   
   

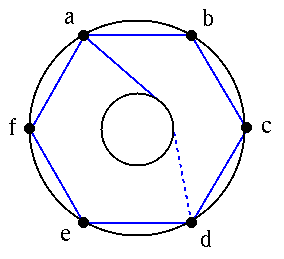
Complete this picture to give an embedded K3,3 on the torus. (The dashed line is the continuation of the solid line, but on the back of the torus.) Compute #V-#E+#F. Does your answer this contradict Euler's formula? Section 1.4 #s 22 (draw all 5), 26 (note K7 contains the other 3 as subgraphs). Section 2.1 # 10. Section 2.2 # 9 a). Section 3.1 # 12.