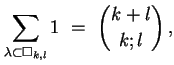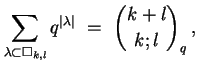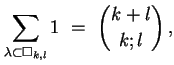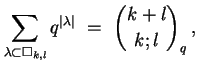First Homework
Math 662, Young Tableaux
28 September, 2004
- Prove that conjugation of Young diagrams induces an
anti-automorphism for the dominance partial order on
partitions.
- Let
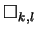 be the partition
be the partition 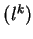 of box shape with
of box shape with
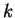 rows and
rows and 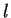 columns.
Adapt the first proof of the identity
to prove the corresponding weighted version
where
columns.
Adapt the first proof of the identity
to prove the corresponding weighted version
where
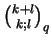 is the
is the 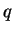 -binomial coefficient of
Gauß.
(Replace each integer
-binomial coefficient of
Gauß.
(Replace each integer 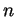 in the definition of the ordinary
binomial coefficient by the
in the definition of the ordinary
binomial coefficient by the 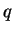 -integer
-integer
 .)
.)
- Prove that the following operations on tableaux commute with
standardization
- Schützenberger's jeu de taquin
- Schensted insertion.
- Formulate and prove a precise statement concerning the
reversibility of Schensted insertion.
- Following the proofs in the course about longest disjoint increasing
subsequences, formulate and prove a result about longest
disjoint decreasing subsequences, and the relation between
increasing and decreasing subsequences.
- Show that column insertion preserves Knuth equivalence of words.
- Prove or disprove: The `switching' defined in the
combinatorial proof that Schur functions are symmetric
defines an action of the infinite symmetric group on tableaux.



Next: About this document ...
Frank Sottile
2004-09-28