Real rational curves in, and from Grassmannians

Séminaire de Géométrie réelle IRMAR Université de Rennes 1 10 Juin 1999 Frank Sottile University of Wisconsin-Madison

   In 1984, Fulton asked how many solutions to a problem of enumerative geometry can be real, when that problem is one of counting geometric figures of some kind having specified position with respect to some general fixed figures. For the problem of plane conics tangent to five general conics, the (surprising) answer is that all 3264 may be real. Such questions arise also in applications; recently, Dietmaier has shown that all 40 positions of the Stewart platform in robotics may be real.

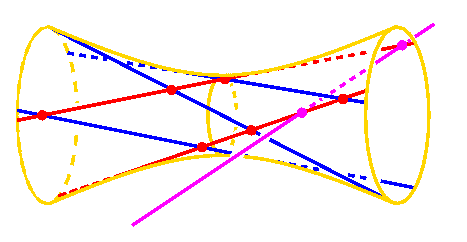
   The purpose of this talk is to give the elementary proof that a certain enumerative problem of counting rational curves on a Grassmannian coming from quantum coholomology can have all of its solutions be real. The proof illustrates a new method, based upon homotopy continuation and using Schuebt induction for finding lower bounds on the maximal numberof real solutions to some enumerative problems. This method is the analog for homogeneous spaces fo Viro's method, or toric deformations. We also use this result to deduce some new results about rational plane curves with maximally many real inflection points.

The picture above shows this phenomenon for the case degree 0 curves in the Grassmannian of lines in projective 3-space, which was known classically.