Phase limit set of a variety

Mounir Nisse and Frank Sottile
A coamoeba is the image of a subvariety of a complex torus (C*)ⁿ under the argument map to the real torus (S¹)ⁿ. Coamoebae exhibit structure that is both polyhdral and curvilinear. We describe the structure of the boundary of the coamoeba of a variety, which we relate to its logarithmic limit set. Detailed examples of lines in three-dimensional space illustrate and motivate these results. This is joint work with Mounir Nisse.

---

Below, we show the coamoebae of a line and a plane in (C*)³. The links are to further pictures and discussion.

---

CoAmoeba of the line t --> (t-1, t-ζ, t-ζ2), where ζ is a primitive third root of 1. More coAmoebae of lines in (C*)3.

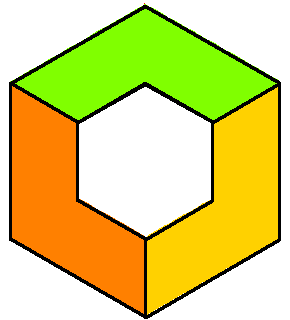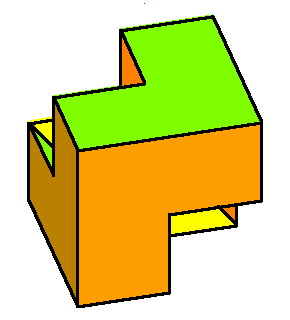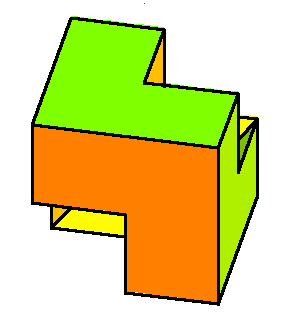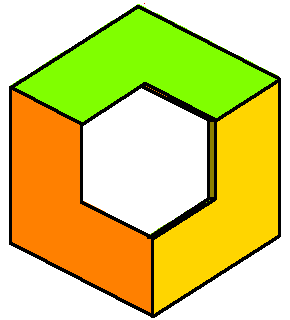CoAmoeba of the plane x+y+z+1 =0 in (C*)3. The coAmoeba of the plane and its phase-limit set.

Last modified: Mon Apr 11 14:56:47 CEST 2011