A problem in the Schubert Calculus
|
In space, there are 2 lines meeting
four given lines (Here in blue,
green, red, and
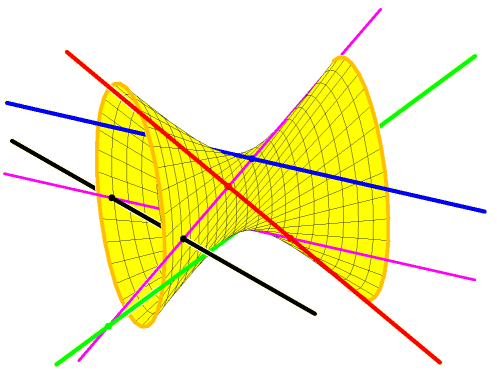
black). Indeed, the blue, green, and red lines are members of one ruling of a unique hyperboloid of one sheet. Members of the other ruling are the lines meeting these three. The fourth black line meets the hyperboloid in two points, and through each of these points is a line meeting our four given lines. If the black line misses the hyperboloid, then the two solutions are complex conjugate. |
|