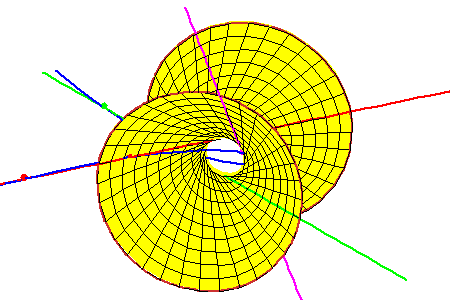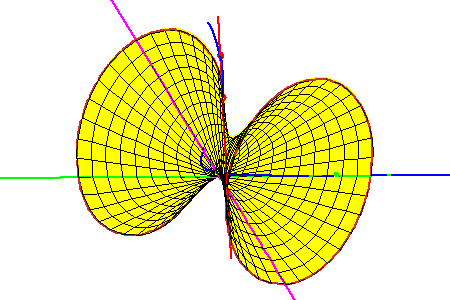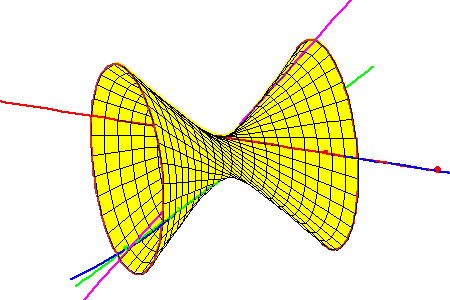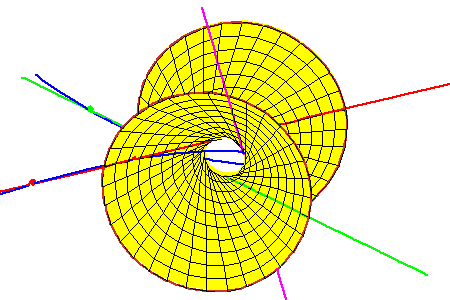
Hyperboloid Through the Three Tangent Lines

---

The lines meeting these three lines form a ruling of a hyperboloid of one sheet that contains the three secant lines. Each intersection of this hyperboloid with a fourth line gives a line meeting all four. In this geometric context, the Secant conjecture is
	equivalent to the following geometric statement: Any line secant along an interval that is disjoint from the intervals of the first three lines meets the hyperboloid in two real points.

---