The Fourth Tangent Line

---

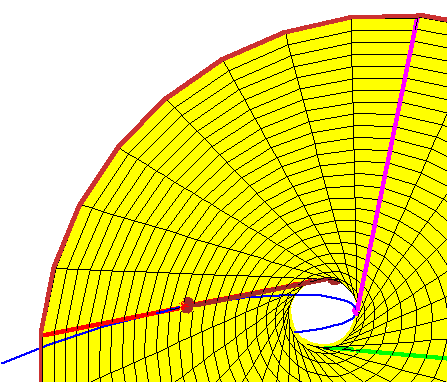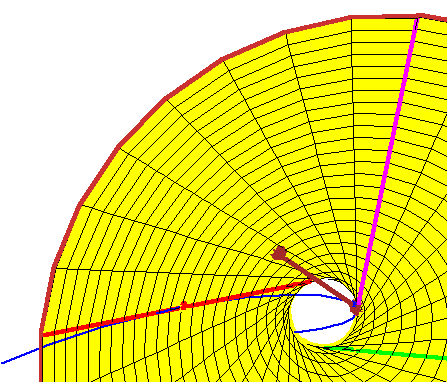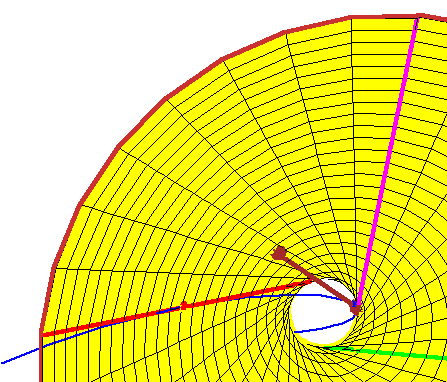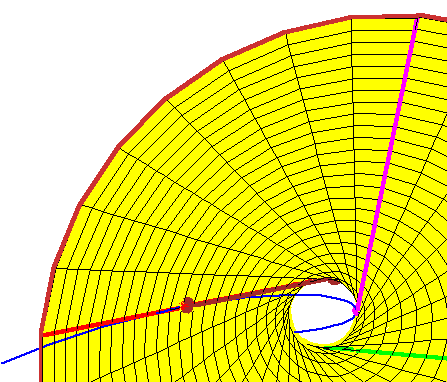
Now consider a fourth line tangent to the rational normal curve. It is sufficient to consider only those lines tangent at a point along the arc between the red and magenta points of tangency of the curve and the hyperboloid.     By now, it should be evident that every such tangent line meets the hyperboloid in two points, which gives two real lines meeting the four given lines that are tangent to the rational normal curve.

---