|
Theorem.
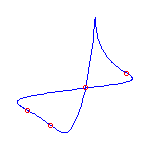
1) A maximally inflected quintic with 4
cusps
and 1 flex has either 1 or 2 (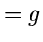 ) real nodes. ) real nodes.
2)
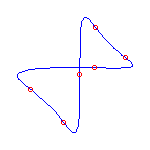
A maximally inflected sextic with 6 cusps
has either 3 or 4 (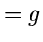 ) real nodes. ) real nodes.
|
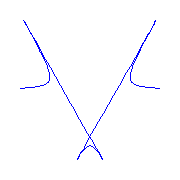
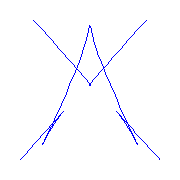
| | 
|
|
Proof:
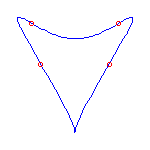
1) Such a curve is dual to a maximally inflected quartic with 1
cusp and 4 flexes.
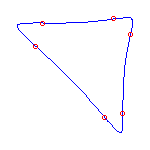
2) Such a curve is dual to a maximally inflected quartic with
6 flexes.
These curves always have the geometry displayed below.
|





