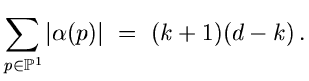|
Multiplicity of ramification
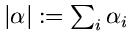
|
|
Theorem. (Eisenbud-Harris)
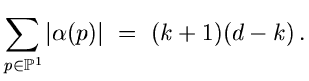
|
|
Enumeration: Given
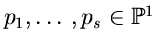 and prescribed
ramification and prescribed
ramification
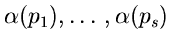
|
|
where
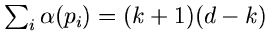 , how many linear series have this
ramification ? , how many linear series have this
ramification ?
Example 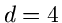 with 6 flexes: (using MAPLE with 6 flexes: (using MAPLE
 )
[Number = 5] )
[Number = 5]
|
|
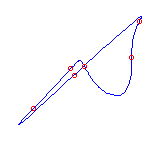
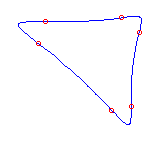
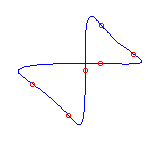
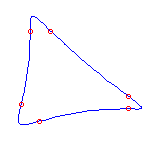
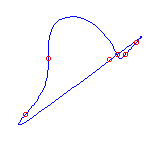
|
|
 (Huber, S.-, Sturmfels, Verschelde)
Numerical methods to compute these linear series: (Huber, S.-, Sturmfels, Verschelde)
Numerical methods to compute these linear series:
|
|
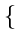 linear series with ramification linear series with ramification 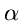 at at 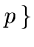
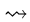 The Schubert variety in Grass The Schubert variety in Grass
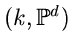
|
|
defined by 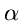 and flag osculating rational normal curve at and flag osculating rational normal curve at 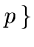 . .
|