
Generic properties of dispersion relations for discrete periodic operators
Ngoc Thanh Do, Peter Kuchment, and Frank Sottile.providing software and additional information on the computations that underlie the proof of the main theorem.

|
Generic properties of dispersion relations for discrete periodic operatorsNgoc Thanh Do, Peter Kuchment, and Frank Sottile. |
| This page accompanies the article
Generic properties of dispersion relations for discrete periodic operators, providing software and additional information on the computations that underlie the proof of the main theorem. |
|
This paper addresses a conjecture about the behaviour of the dispersion relation of
a periodic Schrödinger operator -Δ + V(x), near the edges
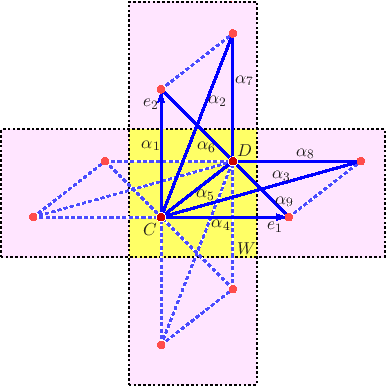
of its spectrum. Roughly, the spectrum should behave like a generic family of self-adjoint matrices. This is an analytic question, but it becomes algebraic when discretized. We address a discrete version concerning a Laplace-Beltrami type operator on the Z2-periodic graph shown in a neighborhood of a fundamental domain at left. Let f be a function on the vertices where f(x+ae1+be2)= z1az2b f(x), where a, b are integers and (z1, z2) ε T2 are unit complex numbers, and e1, e2 are the standard basis vectors of R2. Thus f is determined by its values at the vertices C and D. Let α=(α1,...,α9) be positive real edge weights and let Lα(z) be the finite difference operator defined by This operator Lα(z) is a family (over the parameters α ε R9 and z ε T2) of self-adjoint 2×2 matrices, so it typically has two real eigenvalues λ1≤λ2, which we consider to be functions of z, called band functions. The picture above at left shows the band functions for L(1,2,3,4,5,6,7,8,1)(z), where T2 is the square at the bottom. |
|
| Theorem: The set of α ε R9 for which the band functions λi(z) have nondegenerate extrema contains a non-empty Zariski open subset. | ||
|
The band functions (dispersion relation) are defined implicitly by the characteristic equation for the eigenvalues of
the matrix Lα(z).
Critical points of the band functions are given by implicit derivatives of this characteristic equation, and the
condition that a critical point is nondegenerate is the non-vanishing of a Hessian determinant. The entries of the matrix Lα(z) are linear in the weights α and Laurent monomials in z. As shown in our paper, these conditions for degenerate critical points of the band functions are homogeneous polynomials in α and λ, and Laurent polymnomials in z. Consequently, they define a complex algebraic subscheme V of C10×(C×)2. The set of real parameters α for which Lα(z) has degenerate extrema is a subset of the real points of the projection of V to C9α. Here, we document several computations that give proofs of the Theorem, as well as investigate some further questions. |
||
Let us first recall the matrix A(α1,...α9,z1,z2) =
A:=(aij), for i,j=1,2.
| ||||||||||||||||
|
There are four equations. The first is the characteristic equation for the eigenvalues λ of the matrix
A(α1,...α9,z1,z2).
Then there are two implicit equations for ∂λ/∂zi for i=1,2.
The fourth equation is the Hessian determinant for the second (implicit) partial derivatives of λ with respect to the zi.
Implicit differentiation represents the implicit derivative as a rational expression of the parameters and variables. Since our formulation is that these implicit derivatives vanish, we only take the numerators of the rational expressions. This may introduce some extraneous solutions. We used a Maple script, Bertini.maple to generate these equations, and to write an input file Bertini_input for the computation in bertini. Running the file Bertini.maple creates the input file Bertini_input, we also have what this run dumps to a VT100 terminal, in Bertini_output. Follow this link for details of the Bertini computation that establishes Theorem ???. | ||||||||||||||||
|
We proved Theorem ?? with a symbolic computation that showed when
(α1,α2,...,α8,α9)=(1,2,3,4,5,6,7,8,1),
all critical points are nondegenerate.
This computation may be done by running the Maple file Empty.maple; it generates the
equations and then shows that they define the idea <1>, which means there are no solutions.
There is a version for the computer algebra system Singular, it is the file
Empty.sing.
We also investigated all subgraphs which consistently gave degenerate dispersion relations. The file for that computation is Subsets.maple and its output is Subsets_out. For each subset S of the edges, it computes 10 random instances of the equations for degenerate critical points for the graph whose edges are chosen from S. If for each of these 10 instances, it finds degenerate critical points, then it saves that subset and writes it to the standard output. We captured that in the file Subsets_out. There were 87 'degenerate' subgraphs. We analyzed that file, finding eleven maximal 'degenerate' subgraphs, which were displayed in our paper. While each 'degenerate' subgraph was disconnected, not all disconnected subgraphs were 'degenerate'. For that, we used Components.maple to compute all disconnected subgraphs. Some procedures it used are in the file ComponentsP.maple, which is needed to run Components.maple. Here is its output: Components_out. We also wrote a short file to find the disconnected subgraphs whose dispersion relation was nondegenerate: Compare.maple. |

| Last modified: Sun Aug 18 17:08:52 CDT 2019 |