Note that a polynomial of the form (§) has l + 2k + kp complex zeroes. These data suggest that the maximum number of real roots for a univariate polynomial of the form (§) is bounded by 3k+c, where c is some constant. In fact, we have a construction of such a polynomial with 4k+2 (or 4k+1 depending on the parity of l) real zeroes.
    This experimentation is part of a research project we engaged in at the MSRI as part of the program on Topological Aspects of Real Algebraic Geometry. It will result in a publication: "Polynomial systems with few real zeroes".

Such a polynomial is the univariate eliminant of a polynomial system whose support is the near circuit which consists of the four integer points (0,0,0), (1,0,0), (0,1,0), and (1,p,q) in R3, and the segment (0,0,0), (0,0,-1), ..., (0,0,-k). When p and q are relatively prime, the first four vectors are the vertices of an empty simplex. The first four points and (0,0,-k) are in convex position if q-pk-k>0.     We apply the affine transformation z |---> z + k(1-x-y), and then set l:=q-pk-k. When l>0, this point configuration lies in the positive octant. It is the column vectors of the matrix 0 0 0 ... 0 1 0 1 0 0 0 ... 0 0 1 p 0 1 2 ... k 0 0 l and a polynomial system with this support is equivalent to the following system x = f(z) y = g(z) xy pz lz k = h(z) Substituting  f(z) for x and g(z) for y gives the univariate eliminant   f(z)(g(z)) p z k+l - h(z). This polynomial makes sense if k+l >=0. If k+l<0, then we multiply this Laurent polynomial by z-k-l to turn it into a polynomial.

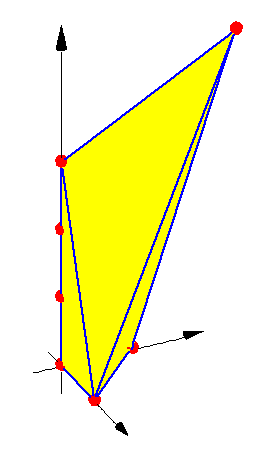
The polytope when (k, p, l)  =  (3,2,5).