Viro's Construction: 5

Viro's Construction: A Sextic (d=6)

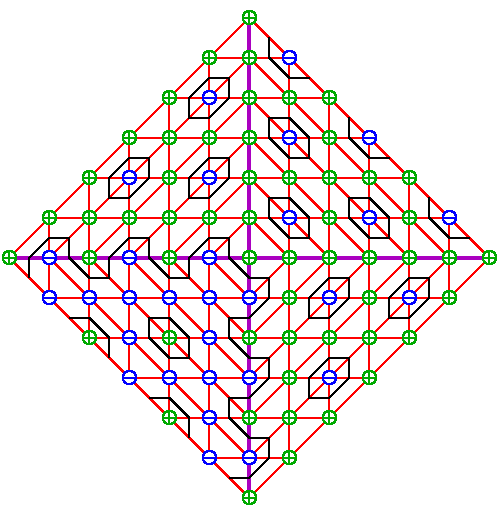Begin with a regular triangulation P_w of
{(x,y) | 0 <= x,y and x+y <= 6} whose vertices are the lattice points

Reflecting P_w in the axes gives its Newton diagram.

A T-curve depends upon signs

and

placed at the vertices of the triangulation P_w.

Extend the signs to the Newton diagram, reflecting each sign and changing those an odd distance from the reflecting axis.

Finally, in the triangles whose vertices have different signs, draw a line connecting the midpoints of the edges with differing signs.
In this way, we obtain the desired T-curve.

This particular construction gives the Harnack Sextic.