The two lines meeting 4 lines in 3-space

Meaning of Picture: This picture shows that given 4 general lines (3 blue and one maroon) in ordinary 3-space, there will be two lines meeting all four.

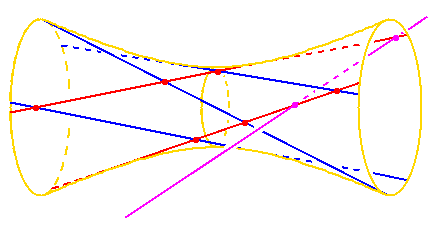
One way to see this is to first consider the 3 blue lines. If they are mutually skew, they will lie on a hyperboloid of one sheet. On the hyperboloid of one sheet, there are two families of lines, and each member of one family meets every member of the other family. The blue lines are in one family, and the set of lines which meet all 3 blue lines is the other family (in red). If we now consider the fourth maroon line, it will meet the hyperboloid in two points, the maroon dots. Through each of these maroon dots there will be a unique line in the second family. These two lines are the two lines which meet our four given lines.

The Reality of this discussion.

The careful reader will note that the maroon line need not intersect the hyperboloid in two points---besides the case of tangency (which gives rise to a solution counted with multiplicity 2)---it could be disjoint from the hyperboloid. This shows that the proper setting for this problem is over the complex numbers, where the maroon line will always meet the hyperboloid. This is a manifestation of a general fact: over the complex numbers, enumerative geometric questions of this sort always have the same number of solutions.

This picture illustrates a feature of the real numbers, that the number of solutions to such questions may depend upon subtle properties of the configurations of the conditions. It is in general a difficult problem to determine how many real solutions there are. An upper bound is given by the number of complex solutions. One may ask:

When is this upper bound attained by real solutions?

A recent theorem of says that this upper bound is reached on many problems in enumerative geometry that arise from Schubert's calculus. It is also attained for certain problems of counting rational curves in a Grassmann variety, and for many problems involving flags.