Next: 6.ii. Curves With Maximally Many Solitary Points
Up: 6. Classical Constructions

6.i. Curves With Maximally Many Real Nodes

We construct maximally inflected curves of degree d with the maximum number (d-1)(d-2)/2 nodes by deforming a particular reducible curve in a precise way using Shustin's theory [Sh99] to control the singularities in the deformation. The idea for this comes from the two degree 4 curves pictured below. The curve on the right is a deformation of the reducible curve on the left.

Specifically, the reducible curve is defined by xy (3(x - y)² + (3x + 3y - 4)² - 4) = 0 , and is the union of the 2 coordinate axes and an ellipse. The curve on the right is defined by the polynomial obtained by subtracting (1/20)(x + y)²(x + y - 1)² from the equation of the reducible curve. This deforming term defines two parallel lines passing through the singularities of the reducible curve.

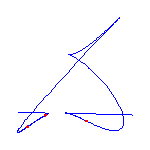
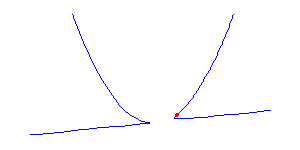
The quartic curve on the right has 2 solitary points at (1,0) and (0,1) and a node at the origin. By the genus formula, it is rational. It also has 6 flexes. Four are indicated by circles, and there is one more along each asymptote, as the curvature of the segment of the curve along the asymptote is different in each of the visible branches. (The tubular neighborhood of an axis is a Möbius band.) Thus any parameterization of this curve is a maximally inflected quartic with 6 flexes, 1 node, and 2 solitary points.

The more sophisticated ideas needed for the general construction are provided by Shustin's theory. We describe the ingredients of this deformation, verify that it is valid, and lastly show that the curve we constructed has the desired properties. Fix an integer d > 2 throughout and let P₀ be the union of a conic and any d-2 distinct lines tangent to the conic. Then P₀ is a reducible curve of degree d. Each pair of tangents meet and no three meet in a point as the dual curve to the conic is another conic. Thus P₀ has (d-2)(d-3)/2 simple nodes and d-2 other singularities at the points of tangency. We deform those tangency singularities while preserving the nodes.

In a neighborhood V of each point of tangency, P_d is isomorphic to the reducible curve K₀ given by the equation

y(y - x²) = 0 , in some neighborhood U of the origin. For each t in R, let K_t be the deformation of K₀ defined in U by

y(y - x²) + tx² = 0 .

(1)

For t positive but sufficiently small, K_t has a solitary point at the origin and 2 flexes along each branch near the parabola y=x², but within U. Moreover, it lies above the x-axis. We display the reducible curve on the left and the deformation K_t for t=1/15 on the right.

If a certain cohomology group vanishes, then Shustin's Theorem [Theorem 1 in Sh99] guarantees the existence of a real number e>0 and of a deformation P_t of the curve P₀ for t in the interval (0,e) such that (1) P_t has degree d, (2) P_t has a node in a neighbourhood of each node of P₀, and (3) in a neighborhood V of each point of tangency of P₀, P_t is isomorphic to K_t, in the neighborhood U of the origin. Another result of Shustin [Lemma 3 in Sh99] gives the numerical criterion for the vanishing of this cohomology group

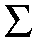(deg X_z - isd_z) < 4(d-1) ,

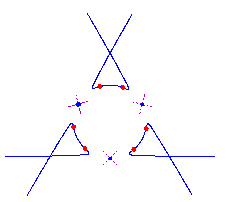
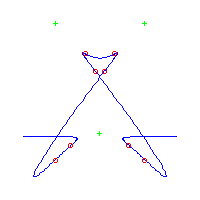
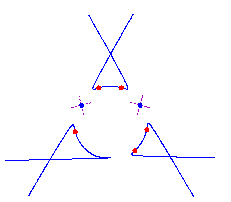
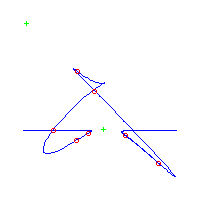
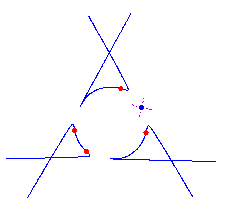
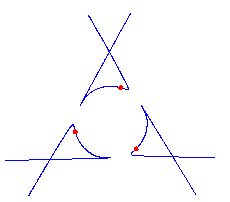
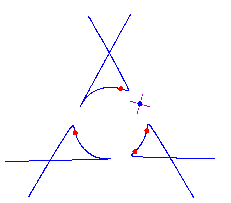
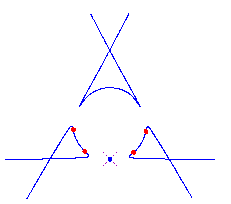
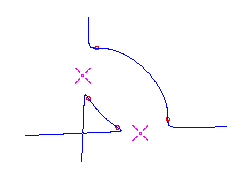
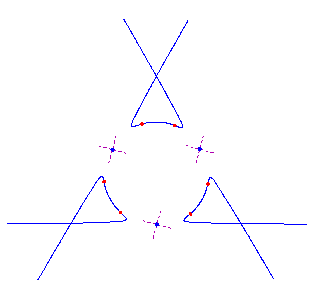
the sum over all singular points z of the curve P₀, where X_z is the scheme of the singularity z and isd_z is a positive integer. When z is a node, X_z has multiplicity 1, and when z is a point of tangency, X_z has multiplicity 2. Thus the above sum is at most d-2, and so the deformation exists.

For 0 < t < e, the curve P_t has (d-2)(d-3)/2 nodes and d-2 solitary points, by the construction. Since it has degree d, it is rational. Also from the construction, we see that each solitary point contributes 2 flexes, accounting for 2(d-2) flexes. Furthermore, there is an additional flex along each asymptote (the original tangent lines) as the concavity of P_t changes while passing through infinity. Thus any parameterization of the curve P_t gives a maximally inflected curve of degree d with 3(d-2) flexes, (d-2)(d-3)/2 nodes and d-2 solitary points. Here is a picture of the reducible curve and the maximally inflected deformation, when d=5.

Theorem. For each k between 0 and d-2, there is a maximally inflected curve with k cusps, 3(d-2)-2k flexes, d-2-k solitary points, and (d-2)(d-3)/2 nodes.

Proof . In the previous construction, we may replace the local model K_t defined in (1) by the local model L_t defined by

y(y - x²) + tx³ = 0 .

(2)

For t > 0, L_t has a cusp at the origin and one flex near the origin. We display L_t for t=1/10 with the singular curve L ₀ on the left.

For every tangency point where we use the local perturbation L_t, we will get a cusp, no solitary point, and only one flex; the flex along the tangent line does not appear, as the concavity of L_t does not change along that line.

The result follows as we may do this for any of the d-2 tangency points.

For t > 0, the cusp in the curve L_t (2) is on the branch to the left of the origin. Had we instead used the perturbation M_t given by

y(y - x²) - tx³ = 0 , then the cusp is now on the right branch for t>0. There are 3^d-2 different ways to use one of these three local models K_t, L_t, or M_t for the perturbation of the tangency singularities. Not all give topologically distinct curves, as there are some symmetries; for example, each of the 2(d-2) ways to have a single cusp are the same topologically. Also, not all possibilities for ordering of cusps and flexes along the curve P_t is possible; On any such curve, each cusp is either preceded or followed by a flex. Thus for instance, we cannot obtain three consecutive cusps with this construction.

Here are pictures of some of the quintics that we can construct by this method. The first three are paired with pictures of quintics that were computed and drawn numerically.

Next: 6.ii. Curves With Maximally Many Solitary Points
Up: 6. Classical Constructions