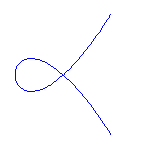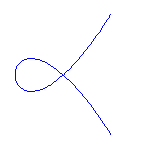Previous: 2 Pictures of Ramification
Next: 4. Maximally Inflected Quartics
Up: Table of Contents
3. Maximally Inflected Cubics
Up to projective transformation,
there are only three real rational plane curves.
They are represented by the
equations
y2 = x3+x2,
y2 = x3-x2, and
y2 = x3,
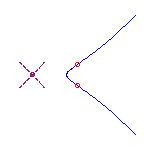
and they have the shapes shown below.
Real rational cubics
All three have a real flex at infinity and are singular at the origin.
The first has a real node and no other real flexes, the second has
a solitary point and two real flexes, which we indicate by dots
and the complex tangents at the solitary point with dashed lines.
The third has a real cusp.
The last two are maximally inflected, while the
first is not.
In general, the number of real nodes is restricted for maximally inflected
curves.



Previous: 2 Pictures of Ramification
Next: 4. Maximally Inflected Quartics
Up: Table of Contents