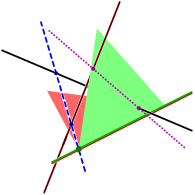
We present a new numerical homotopy continuation algorithm for finding
all solutions to Schubert problems on Grassmannians.
This Littlewood-Richardson homotopy is based on Vakil's geometric proof
of the Littlewood-Richardson rule.
Its start solutions are given by linear equations and they are tracked
through a sequence of homotopies encoded by certain checker configurations
to find the solutions to a given Schubert problem.
For generic Schubert problems the number of paths tracked is optimal.
The Littlewood-Richardson homotopy algorithm is implemented
using the path trackers of the software package PHCpack.
|