Two Murnaghan-Nakayama Rules in Schubert Calculus
Andrew Morrison and Frank Sottile
p4*σ(3,2,1) = σ(3,3,3,2) + σ(4,4,3) - qσ(3) - qσ(1,1,1)


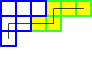
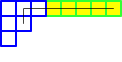
The Murnaghan-Nakayama rule expresses the product of a Schur function with a Newton power sum in the basis of Schur functions. We establish a version of the Murnaghan-Nakayama rule for Schubert polynomials and a version for the quantum cohomology ring of the Grassmannian. These rules compute all intersections of Schubert cycles with tautological classes coming from the Chern character.