
| Phase limit set of a variety |  |
 CoAmoeba of the line t --> (t-1, t-ζ, t-ζ2), where ζ is a primitive third root of 1. More coAmoebae of lines in (C*)3. |
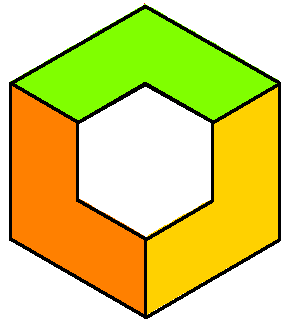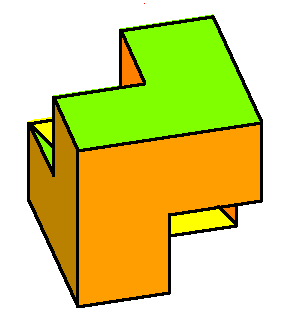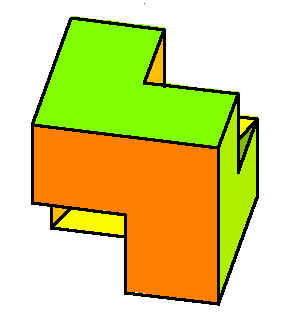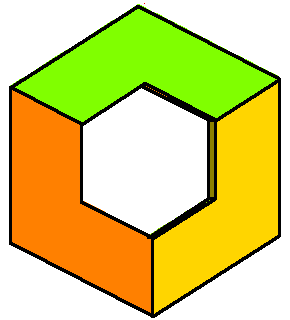 CoAmoeba of the plane x+y+z+1 =0 in (C*)3. The coAmoeba of the plane and its phase-limit set. |